Population Growth: A Mini-Review of Key Concepts

This blog post provides a few resources that should help you review some of the difficult population ecology concepts.  Here a few websites to get you started: 

• Quantitative Population Ecology
• Population Ecology & Exponential Growth (Nat. Geo.)  
• How Populations Grow: The Exponential and Logistic Equations
• Check out relevant chapter resources in the textbook Economy of Nature

Let's start with the basics: Exponential Growth

(Knowledge Library, Nature.com)

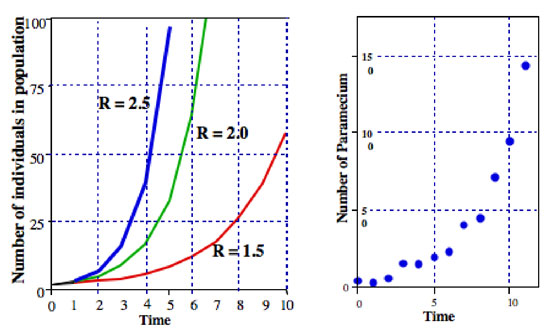
Exponential growth is a type of population growth in which the rate of increase in the number of members is proportional to the number present.


To model exp. growth we use the below formula:

  N(t)= N(0)*(e^(R*t)) 

Where (N(0)): initial population size; (N(t)): the projected population size; R: intrinsic growth rate; and t: an arbitrary time. 

The figure (above right) depicts the extent to which rate (R) affects population size over time (t), given we know the population size at t initial. Note the "J-shaped" growth curve.  (I have not figured out how to use super-/sub-scripts in blogger, sorry!)

Geometric Growth Model

Geometric growth model (equation below) expands upon the exponential growth model by including time (t) as a variable.  Including time as a variable is important for species that have defined growth periods (e.g., breeding season).  

N(t)= N(0)*(R^(t))

When R>1 the population is increasing; R<1 pop. decreasing; R=1 no change in pop. size.

For a more detailed description of how the above equation is derived, and assumptions associated with some of these models visit this website. 

 

Density Dependence

(Knowledge Library, Nature.com)

In the natural world, competition and resource availability limit population growth - this is described as carrying capacity (K).  That is, an environment or ecosystem is only able to support, or "carry", a maximum population size. As the population size approaches carrying capacity, the growth rate slows.  Population growth rate (R) is highest at the inflection point [K/2], after which the growth rate decreases toward zero as N nears K. 

Density dependent factors affecting population size, such as competition or predation are often biotic, whereas density independent limitations are often abiotic, such as environmental stress. 

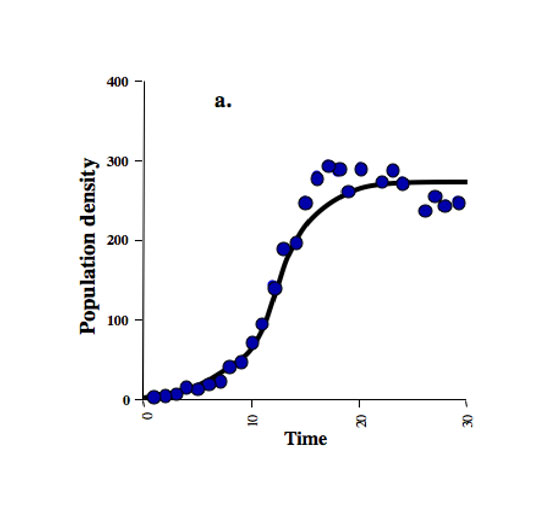
Logistic Population Growth

This equation is density dependent, that is, as the population increases, intraspecific competition increases.  The logistic growth model is a common sigmoid curve or "S-shaped" curve, as seen in the carrying capacity graph above.   

(Knowledge Library, Nature.com)

To find the change in population size over time (dN/dt) while accounting for carrying capacity (K) we use the following equation ("Equation 8").  Where N = population size and r = rate of population change.    

The Allee Effect, or Inverse Density Dependence at Low Density

This effect states that for certain species, when their population is at low densities, there is a positive relationship between population growth rate and density.  That is, decreased population growth is correlated with decreasing abundance, which can result in the population's extinction.  This critical threshold (R=1), or Allee threshold, is the tipping point for a population's survival.

(Ann. Rev. in Ento., 2008)

The many factors that may lead to the Allee Effect have been loosely categorized as follows:

1) Genetic Inbreeding - leading to decreased fitness 

2) Demographic Stochasticity (e.g., sex-ratio fluctuations, or low fecundity)  

3) Reduced intraspecific cooperation when densities are low

In practice, the Allee effect is of concern to conservation biologist.  Instances such as  managing rare species, monitoring species re-introductions, or preventing the establishment of non-native invasive species all  involve small population sizes.  

The most informative description I have found of this phenomenon online (and my source for information) is in this short article by Courcham et al. (1999) published in the scientific journal Trends in Ecology and Evolution (PDF).  

Lotka-Volterra competition model  

Note: The L-V model is Community Ecology and will be included on the final exam.

This model builds on the logistic growth model, by adding a competition coefficient, accounting for a species' ability to inhibit the growth of another (interspecific competition).  The equations below are the logistic growth model as discussed above for individual species (species 1, species 2), but a competition coefficient has been added. 

Competition coefficients may be denoted as alpha or beta, or as in this example, subscripts on the alpha are different.  This coefficient represents the degree to which their competitor may inhibit their growth (alpha) and the size of the competitor's population (N). 

 

(Townsend et al. 2008. Ecology)